Samlet set vil vi dække tre hovedemner i denne lektion:
- Hvad er Tensors og TensorFlow
- Anvendelse af ML-algoritmer med TensorFlow
- TensorFlow brugstilfælde
TensorFlow er en fremragende Python-pakke fra Google, som gør god brug af dataforløbsprogrammeringsparadigmet til stærkt optimerede matematiske beregninger. Nogle af funktionerne i TensorFlow er:
- Distribueret beregningsfunktion, der gør det lettere at administrere data i store sæt
- Dyb læring og neuralt netværkssupport er god
- Det styrer komplekse matematiske strukturer som n-dimensionelle arrays meget effektivt
På grund af alle disse funktioner og rækken af maskinlæringsalgoritmer gør TensorFlow det til et produktionsskala-bibliotek. Lad os dykke ned i koncepter i TensorFlow, så vi kan gøre vores hænder beskidte med kode lige efter.
Installation af TensorFlow
Da vi vil bruge Python API til TensorFlow, er det godt at vide, at det fungerer med begge Python 2.7 og 3.3+ versioner. Lad os installere TensorFlow-biblioteket, inden vi går til de faktiske eksempler og koncepter. Der er to måder at installere denne pakke på. Den første inkluderer brug af Python pakkehåndtering, pip:
pip installere tensorflowDen anden måde vedrører Anaconda, vi kan installere pakken som:
conda install -c conda-smede tensorflowDu er velkommen til at kigge efter natlige builds og GPU-versioner på de officielle TensorFlow-installationssider.
Jeg bruger Anaconda-manager til alle eksemplerne i denne lektion. Jeg lancerer en Jupyter Notebook til det samme:

Nu hvor vi er klar med alle importudtalelser til at skrive en kode, lad os begynde at dykke ned i SciPy-pakken med nogle praktiske eksempler.
Hvad er tensorer?
Tensorer er de grundlæggende datastrukturer, der bruges i Tensorflow. Ja, de er bare en måde at repræsentere data i dyb læring. Lad os visualisere dem her:
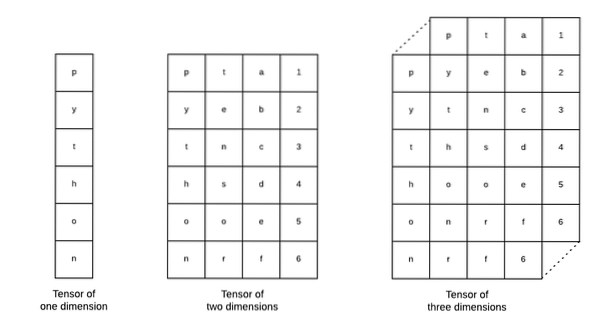
Som beskrevet på billedet, tensorer kan betegnes som n-dimensionelt array som giver os mulighed for at repræsentere data i en kompleks dimension. Vi kan tænke på hver dimension som et andet træk ved data i dyb læring. Dette betyder, at Tensorer kan vokse ud til at være ret komplekse, når det kommer til komplekse datasæt med mange funktioner.
Når vi først ved, hvad Tensorer er, synes jeg det er ret let at udlede, hvad der sker i TensorFlow. Disse vilkår betyder, hvordan tensorer eller funktioner kan strømme i datasæt for at producere værdifuld output, når vi udfører forskellige operationer på det.
Forståelse af TensorFlow med konstanter
Ligesom vi læser ovenfor giver TensorFlow os mulighed for at udføre maskinlæringsalgoritmer på Tensors for at producere værdifuld output. Med TensorFlow er design og træning af Deep Learning-modeller lige frem.
TensorFlow leveres med bygning Beregningsgrafer. Beregningsgrafer er datastrømningsgraferne, hvor matematiske operationer er repræsenteret som noder, og data er repræsenteret som kanter mellem disse noder. Lad os skrive et meget simpelt kodestykke for at give en konkret visualisering:
importer tensorflow som tfx = tf.konstant (5)
y = tf.konstant (6)
z = x * y
udskrive (z)
Når vi kører dette eksempel, ser vi følgende output:
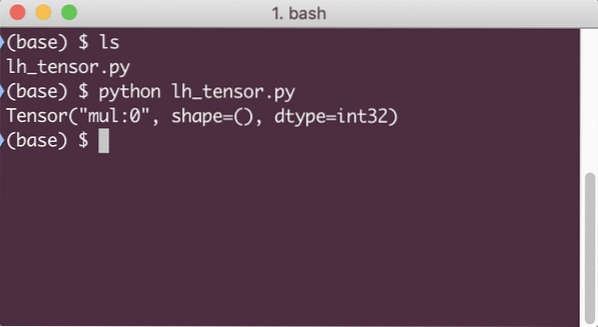
Hvorfor er multiplikationen forkert? Det var ikke, hvad vi forventede. Dette skete, fordi det ikke er sådan, vi kan udføre operationer med TensorFlow. Først skal vi starte en session for at få beregningsgrafen til at fungere,
Med sessioner kan vi indkapsle kontrol af operationer og tilstand af Tensorer. Dette betyder, at en session også kan gemme resultatet af en beregningsgraf, så den kan overføre resultatet til den næste operation i rækkefølgen af udførelsen af rørledningerne. Lad os oprette en session nu for at få det korrekte resultat:
# Start med sessionsobjektetsession = tf.Session()
# Giv beregningen til sessionen og gem den
resultat = session.løb (z)
# Udskriv resultatet af beregningen
print (resultat)
# Luk session
session.tæt()
Denne gang fik vi sessionen og forsynede den med den beregning, den har brug for for at køre på noderne. Når vi kører dette eksempel, ser vi følgende output:
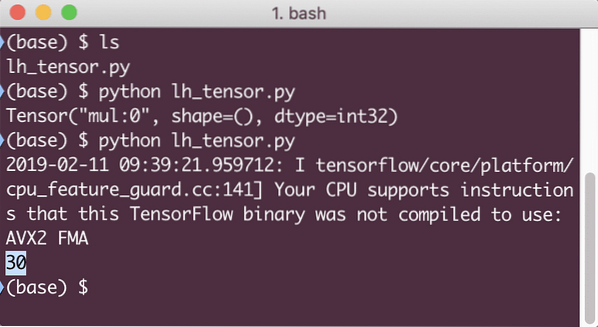
Selvom vi modtog en advarsel fra TensorFlow, fik vi stadig det korrekte output fra beregningen.
Tensoroperationer med et enkelt element
Ligesom hvad vi gangede med to konstante tensorer i det sidste eksempel, har vi mange andre operationer i TensorFlow, som kan udføres på enkeltelementer:
- tilføje
- trække fra
- formere sig
- div
- mod
- abs
- negativ
- skilt
- firkant
- rund
- sqrt
- pow
- eksp
- log
- maksimum
- minimum
- cos
- synd
Enkeltelementoperationer betyder, at selv når du angiver en matrix, udføres operationerne på hvert af elementet i den matrix. For eksempel:
importer tensorflow som tfimporter numpy som np
tensor = np.array ([2, 5, 8])
tensor = tf.convert_to_tensor (tensor, dtype = tf.flyde64)
med tf.Session () som session:
udskrive (session.køre (tf.cos (tensor)))
Når vi kører dette eksempel, ser vi følgende output:
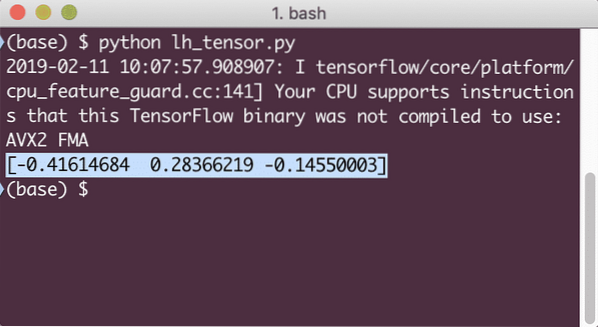
Vi forstod to vigtige begreber her:
- Ethvert NumPy-array kan let konverteres til en Tensor ved hjælp af convert_to_tensor-funktionen
- Operationen blev udført på hvert af NumPy-matrixelementet
Pladsholdere og variabler
I et af de foregående afsnit kiggede vi på, hvordan vi kan bruge Tensorflow-konstanter til at lave beregningsdiagrammer. Men TensorFlow giver os også mulighed for at tage input på flugt, så beregningsgrafen kan være dynamisk. Dette er muligt ved hjælp af pladsholdere og variabler.
Faktisk indeholder pladsholdere ingen data og skal leveres gyldige input i løbetid, og som forventet vil de uden en input generere en fejl.
En pladsholder kan betegnes som en aftale i en graf om, at et input sikkert vil blive leveret ved kørsel. Her er et eksempel på pladsholdere:
importer tensorflow som tf# To pladsholdere
x = tf. pladsholder (tf.flyde32)
y = tf. pladsholder (tf.flyde32)
# Tildeling af multiplikationsoperation w.r.t. -en & b til node mul
z = x * y
# Opret en session
session = tf.Session()
# Pass værdier for pladsholdere
resultat = session.kør (z, x: [2, 5], y: [3, 7])
print ('Multiplikation af x og y:', resultat)
Når vi kører dette eksempel, ser vi følgende output:
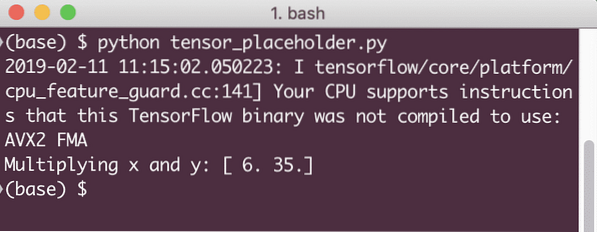
Nu hvor vi har viden om pladsholdere, lad os vende blikket mod variabler. Vi ved, at output fra en ligning kan ændre sig med samme sæt input over tid. Så når vi træner vores modelvariabel, kan den ændre dens adfærd over tid. I dette scenario giver en variabel os mulighed for at tilføje disse parametre, der kan trænes, til vores beregningsgraf. En variabel kan defineres som følger:
x = tf.Variabel ([5.2], dtype = tf.flyde32)I ovenstående ligning er x en variabel, der får sin oprindelige værdi og datatypen. Hvis vi ikke angiver datatypen, udledes den af TensorFlow med dens oprindelige værdi. Se datatyperne til TensorFlow her.
I modsætning til en konstant er vi nødt til at kalde en Python-funktion for at initialisere alle variablerne i en graf:
init = tf.global_variables_initializer ()session.køre (init)
Sørg for at køre ovenstående TensorFlow-funktion, inden vi bruger vores graf.
Lineær regression med TensorFlow
Lineær regression er en af de mest almindelige algoritmer, der bruges til at etablere et forhold i en given kontinuerlig data. Dette forhold mellem koordinatpunkterne, siger x og y, kaldes a hypotese. Når vi taler om lineær regression, er hypotesen en lige linje:
y = mx + cHer er m linjens hældning, og her er det en vektor, der repræsenterer vægte. c er den konstante koefficient (y-skæring) og her repræsenterer den Partiskhed. Vægten og bias kaldes parametre for modellen.
Lineære regressioner giver os mulighed for at estimere værdierne for vægt og bias, så vi har et minimum omkostningsfunktion. Endelig er x den uafhængige variabel i ligningen, og y er den afhængige variabel. Lad os nu begynde at opbygge den lineære model i TensorFlow med et simpelt kodestykke, som vi vil forklare:
importer tensorflow som tf# Variabler til parameterhældning (W) med startværdi som 1.1
W = tf.Variabel ([1.1], tf.flyde32)
# Variabel for bias (b) med startværdi som -1.1
b = tf.Variabel ([- 1.1], tf.flyde32)
# Pladsholdere til at levere input eller uafhængig variabel, betegnet med x
x = tf.pladsholder (tf.flyde32)
# Ligningsligning eller lineær regression
lineær_model = W * x + b
# Initialisering af alle variabler
session = tf.Session()
init = tf.global_variables_initializer ()
session.køre (init)
# Udfør regressionsmodel
udskrive (session.kør (lineær_model x: [2, 5, 7, 9]))
Her gjorde vi netop det, vi forklarede tidligere, lad os sammenfatte her:
- Vi startede med at importere TensorFlow til vores script
- Opret nogle variabler til at repræsentere vektorvægten og parameterbias
- En pladsholder er nødvendig for at repræsentere input, x
- Repræsentere den lineære model
- Initialiser alle de nødvendige værdier til modellen
Når vi kører dette eksempel, ser vi følgende output:
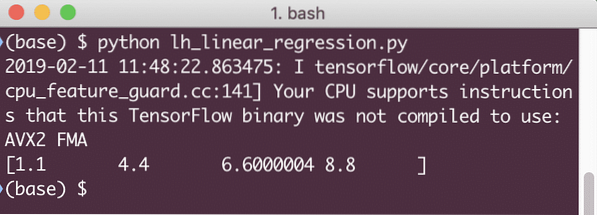
Det enkle kodestykke giver bare en grundlæggende idé om, hvordan vi kan opbygge en regressionsmodel. Men vi er stadig nødt til at gøre nogle flere trin for at færdiggøre den model, vi byggede:
- Vi er nødt til at gøre vores model selvuddannelig, så den kan producere output til enhver given input
- Vi er nødt til at validere output leveret af modellen ved at sammenligne det med den forventede output for givne x
Tabsfunktion og modelvalidering
For at validere modellen skal vi have et mål for, hvor afvigende strømoutput er fra det forventede output. Der er forskellige tabsfunktioner, som kan bruges her til validering, men vi vil se på en af de mest almindelige metoder, Summen af kvadratfejl eller SSE.
Ligningen for SSE er givet som:
E = 1/2 * (t - y) 2Her:
- E = gennemsnitlig kvadratfejl
- t = Modtaget output
- y = forventet output
- t - y = Fejl
Lad os nu skrive et kodestykke i forlængelse af det sidste uddrag for at afspejle tabsværdien:
y = tf.pladsholder (tf.flyde32)fejl = lineær_model - y
squared_errors = tf.firkant (fejl)
tab = tf.reducer_sum (firkantede_fejl)
udskrive (session.run (tab, x: [2, 5, 7, 9], y: [2, 4, 6, 8]))
Når vi kører dette eksempel, ser vi følgende output:
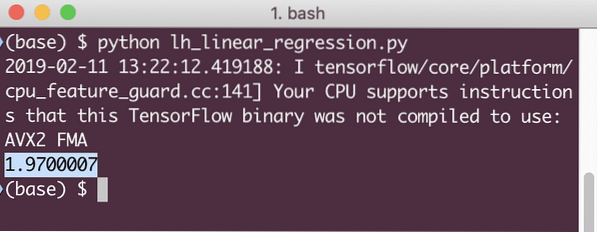
Det er klart, at tabsværdien er meget lav for den givne lineære regressionsmodel.
Konklusion
I denne lektion kiggede vi på en af de mest populære Deep learning- og Machine learning-pakker, TensorFlow. Vi lavede også en lineær regressionsmodel, som havde meget høj nøjagtighed.
 Phenquestions
Phenquestions