PyTorch Tutorial med lineær regression

PyTorch er en Python-baseret videnskabelig pakke, der giver en udskiftning af NumPy ndarrays som Tensorer, der drager størst fordel af GPU'erne. Et andet positivt punkt omkring PyTorch-rammen er den hastighed og fleksibilitet, den giver under computing. PyTorch er et effektivt alternativ til at arbejde med Tensors ved hjælp af Tensorflow, som vi studerede om tidligere.

PyTorch har få store fordele som en beregningspakke, såsom:

Det er muligt at oprette beregningsgrafer, mens vi går. Dette betyder, at det ikke er nødvendigt at vide på forhånd om grafens hukommelseskrav. Vi kan frit oprette et neuralt netværk og evaluere det i løbetid.
Let at Python API, som let kan integreres
Støttet af Facebook, så samfundsstøtten er meget stærk
Giver indbygget multi-GPU-support

PyTorch omfavnes hovedsageligt af Data Science-samfundet på grund af dets evne til nemt at definere neurale netværk. Lad os se denne beregningspakke i aktion i denne lektion.

Installation af PyTorch

Bare en note, før du starter, kan du bruge et virtuelt miljø til denne lektion, som vi kan lave med følgende kommando:

python -m virtualenv pytorch
kilde pytorch / bin / aktiver

Når det virtuelle miljø er aktivt, kan du installere PyTorch-biblioteket i den virtuelle env, så eksempler, vi opretter næste, kan udføres:

pip installer pytorch

Vi bruger Anaconda og Jupyter i denne lektion. Hvis du vil installere det på din maskine, skal du se på lektionen, der beskriver “Sådan installeres Anaconda Python på Ubuntu 18.04 LTS ”og del din feedback, hvis du står over for problemer. For at installere PyTorch med Anaconda skal du bruge følgende kommando i terminalen fra Anaconda:

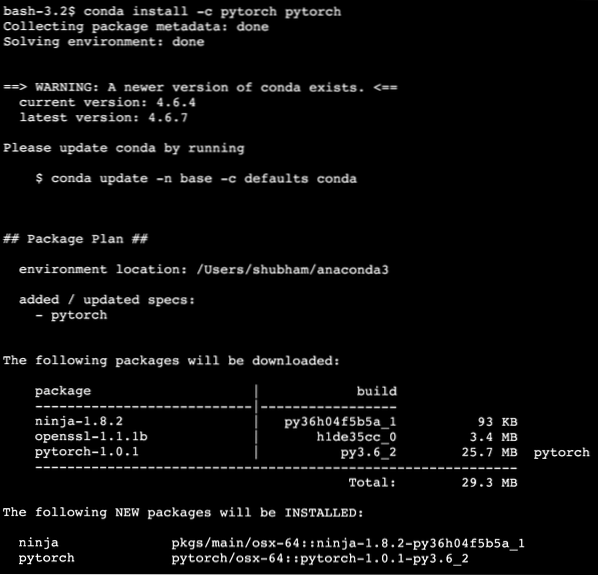
conda install -c pytorch pytorch

Vi ser noget som dette, når vi udfører ovenstående kommando:

Når alle de nødvendige pakker er installeret og færdige, kan vi komme i gang med at bruge PyTorch-biblioteket med følgende importerklæring:

importer fakkel

Lad os komme i gang med grundlæggende PyTorch-eksempler, nu hvor vi har forudsætningspakkerne installeret.

Kom godt i gang med PyTorch

Da vi ved, at neurale netværk grundlæggende kan struktureres, da Tensorer og PyTorch er bygget op omkring tensorer, har der tendens til at være et betydeligt løft i ydeevne. Vi kommer i gang med PyTorch ved først at undersøge, hvilken type tensorer den giver. For at komme i gang med dette skal du importere de nødvendige pakker:

importer fakkel

Dernæst kan vi definere en ikke-initialiseret Tensor med en defineret størrelse:

x = fakkel.tom (4, 4)
print ("Array Type: ".format (x.type)) # type
print ("Array Shape: ".format (x.form)) # form
udskrive (x)

Vi ser noget som dette, når vi udfører ovenstående script:

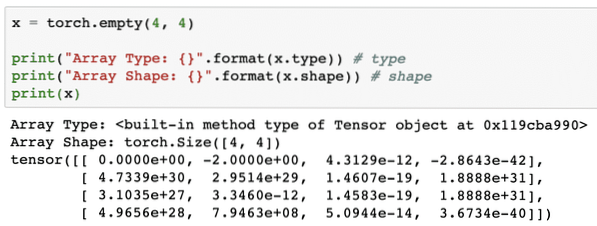
Vi lavede netop en ikke-initialiseret Tensor med en defineret størrelse i ovenstående script. At gentage fra vores Tensorflow-lektion, tensorer kan betegnes som n-dimensionelt array som giver os mulighed for at repræsentere data i en kompleks dimension.

Lad os køre et andet eksempel, hvor vi initialiserer en Torched tensor med tilfældige værdier:

random_tensor = lommelygte.rand (5, 4)
udskriv (tilfældig_tensor)

Når vi kører ovenstående kode, ser vi et tilfældigt tensorobjekt udskrevet:

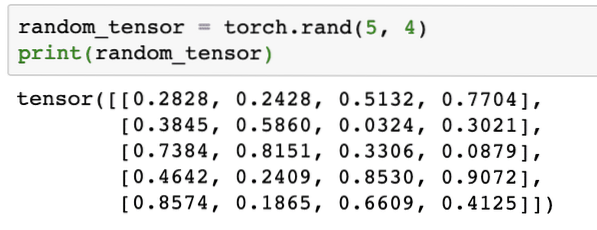
Bemærk, at output for ovenstående tilfældige Tensor kan være anderledes for dig, fordi det er tilfældigt !

Konvertering mellem NumPy og PyTorch

NumPy og PyTorch er fuldstændig kompatible med hinanden. Derfor er det let at omdanne NumPy-arrays til tensorer og omvendt. Bortset fra den lethed, API giver, er det sandsynligvis lettere at visualisere tensorer i form af NumPy-arrays i stedet for Tensors, eller bare kalde det min kærlighed til NumPy!

For eksempel importerer vi NumPy til vores script og definerer et simpelt tilfældigt array:

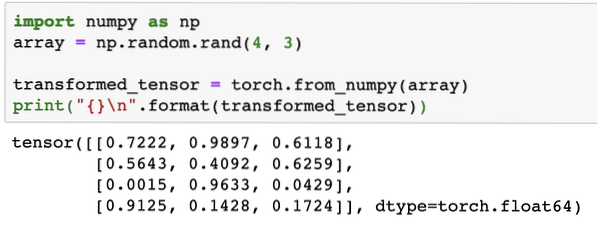
importer numpy som np
matrix = np.tilfældig.rand (4, 3)
transformed_tensor = fakkel.from_numpy (array)
udskriv (" \ n".format (transformeret_tensor))

Når vi kører ovenstående kode, ser vi det transformerede tensorobjekt udskrevet:

Lad os nu prøve at konvertere denne tensor tilbage til et NumPy-array:

numpy_arr = transformeret_tensor.bedøvet ()
udskriv (" \ n".format (type (numpy_arr), numpy_arr))

Når vi kører ovenstående kode, ser vi det transformerede NumPy-array udskrevet:

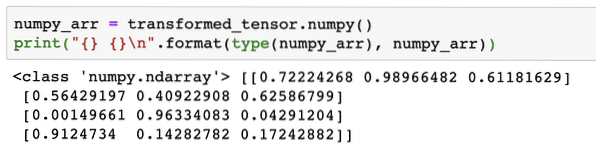
Hvis vi ser nøje, opretholdes selv nøjagtigheden af konvertering, mens vi konverterer arrayet til en tensor og derefter konverterer det tilbage til et NumPy-array.

Tensoroperationer

Før vi begynder vores diskussion omkring neurale netværk, bør vi kende de operationer, der kan udføres på Tensorer, mens vi træner neurale netværk. Vi vil også bruge udvidet NumPy-modul.

Udskæring af en tensor

Vi har allerede set hvordan vi laver en ny Tensor, lad os lave en nu og skive det:

vektor = fakkel.tensor ([1, 2, 3, 4, 5, 6])
print (vektor [1: 4])

Ovenstående kodestykke giver os følgende output:

tensor ([2, 3, 4])

Vi kan ignorere det sidste indeks:

print (vektor [1:])

Og vi kommer også tilbage, hvad der forventes med en Python-liste:

tensor ([2, 3, 4, 5, 6])

Oprettelse af en flydende tensor

Lad os nu lave en flydende Tensor:

float_vector = fakkel.FloatTensor ([1, 2, 3, 4, 5, 6])
udskriv (float_vector)

Ovenstående kodestykke giver os følgende output:

tensor ([1., 2., 3., 4., 5., 6.])

Type af denne Tensor vil være:

udskrive (float_vector.dtype)

Giver tilbage:

fakkel.flyde32

Aritmetiske operationer på tensorer

Vi kan tilføje to tensorer ligesom alle matematiske elementer, som:

tensor_1 = fakkel.tensor ([2, 3, 4])
tensor_2 = fakkel.tensor ([3, 4, 5])
tensor_1 + tensor_2

Ovenstående kodestykke giver os:

Vi kan formere sig en tensor med en skalar:

tensor_1 * 5

Dette vil give os:

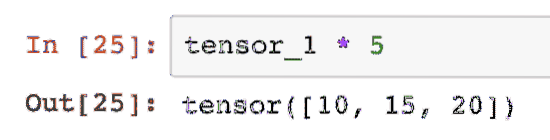
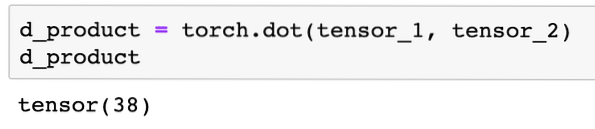
Vi kan udføre en prikprodukt mellem to tensorer også:

d_product = fakkel.prik (tensor_1, tensor_2)
d_product

Ovenstående kodestykke giver os følgende output:

I næste afsnit vil vi se på højere dimension af Tensorer og matricer.

Matrixmultiplikation

I dette afsnit vil vi se, hvordan vi kan definere målinger som tensorer og multiplicere dem, ligesom vi plejede at gøre i gymnasiets matematik.

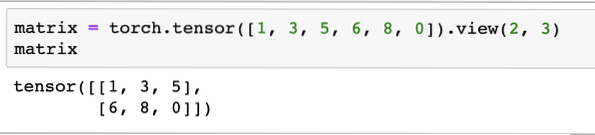
Vi definerer en matrix til at starte med:

matrix = fakkel.tensor ([1, 3, 5, 6, 8, 0]).udsigt (2, 3)

I ovenstående kodestykke definerede vi en matrix med tensorfunktionen og derefter specificeret med se funktion at den skal laves som en 2-dimensionel tensor med 2 rækker og 3 kolonner. Vi kan give flere argumenter til udsigt funktion til at specificere flere dimensioner. Bare bemærk at:

rækkeoptælling ganget med kolonneantal = varetal

Når vi visualiserer ovennævnte 2-dimensionelle tensor, ser vi følgende matrix:

Vi definerer en anden identisk matrix med en anden form:

matrix_b = fakkel.tensor ([1, 3, 5, 6, 8, 0]).udsigt (3, 2)

Vi kan endelig udføre multiplikationen nu:

fakkel.matmul (matrix, matrix_b)

Ovenstående kodestykke giver os følgende output:

Lineær regression med PyTorch

Lineær regression er en maskinlæringsalgoritme baseret på overvågede læringsteknikker til at udføre regressionsanalyse på uafhængige og en afhængig variabel. Forvirret allerede? Lad os definere lineær regression i enkle ord.

Lineær regression er en teknik til at finde ud af forholdet mellem to variabler og forudsige, hvor meget ændring i den uafhængige variabel forårsager, hvor meget ændring i den afhængige variabel. For eksempel kan lineær regressionsalgoritme anvendes til at finde ud af, hvor meget prisstigninger for et hus, når dets areal øges med en bestemt værdi. Eller hvor meget hestekræfter i en bil, der er til stede baseret på dens motorvægt. Det andet eksempel lyder måske underligt, men du kan altid prøve underlige ting, og hvem ved, at du er i stand til at etablere et forhold mellem disse parametre med lineær regression!

Den lineære regressionsteknik bruger normalt ligningen af en linje til at repræsentere forholdet mellem den afhængige variabel (y) og den uafhængige variabel (x):

y = m * x + c

I ovenstående ligning:

m = kurvens hældning
c = bias (punkt, der skærer y-aksen)

Nu hvor vi har en ligning, der repræsenterer forholdet mellem vores brugssag, vil vi forsøge at oprette nogle eksempeldata sammen med en plotvisualisering. Her er eksemplerdata for huspriser og deres størrelser:

house_prices_array = [3, 4, 5, 6, 7, 8, 9]
house_price_np = np.array (house_prices_array, dtype = np.flyde32)
house_price_np = hus_pris_np.omforme (-1,1)
house_price_tensor = Variabel (fakkel.from_numpy (house_price_np))
husstørrelse = [7.5, 7, 6.5, 6.0, 5.5, 5.0, 4.5]
house_size_np = np.matrix (husstørrelse, dtype = np.flyde32)
house_size_np = house_size_np.omforme (-1, 1)
house_size_tensor = Variabel (fakkel.from_numpy (house_size_np))
# lader os visualisere vores data
importer matplotlib.pyplot som plt
plt.spredning (husprispriser, husstørrelse_np)
plt.xlabel ("Huspris $")
plt.ylabel ("Husstørrelser")
plt.titel ("Huspris $ VS Husstørrelse")
plt

Bemærk, at vi brugte Matplotlib, som er et fremragende visualiseringsbibliotek. Læs mere om det i Matplotlib Tutorial. Vi ser følgende grafplot, når vi kører ovenstående kodestykke:

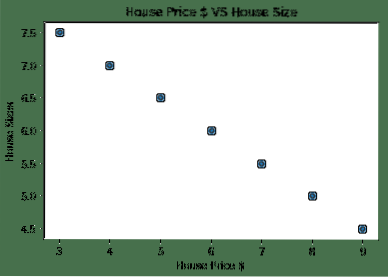
Når vi laver en linje gennem punkterne, er det måske ikke perfekt, men det er stadig nok til den slags forhold, variablerne har. Nu hvor vi har samlet og visualiseret vores data, vil vi forudsige, at hvad der vil være husets størrelse, hvis det blev solgt for $ 650.000.

Målet med at anvende lineær regression er at finde en linje, der passer til vores data med minimal fejl. Her er de trin, vi vil udføre for at anvende den lineære regressionsalgoritme til vores data:

Konstruer en klasse for lineær regression
Definer modellen fra denne klasse for lineær regression
Beregn MSE (middel kvadratfejl)
Udfør optimering for at reducere fejlen (SGD i.e. stokastisk gradient nedstigning)
Udfør Backpropagation
Endelig, forudsig

Lad os begynde at anvende ovenstående trin med korrekt import:

importer fakkel
fra fakkel.autograd import Variabel
importer fakkel.nn som nn

Dernæst kan vi definere vores lineære regressionsklasse, der arver fra PyTorch neurale netværksmodul:

klasse LineærRegression (nn.Modul):
def __init __ (selv, input_størrelse, output_størrelse):
# superfunktion arver fra nn.Modul, så vi kan få adgang til alt fra nn.Modul
super (Lineærregression, selv).__i det__()
# Lineær funktion
selv.lineær = nn.Lineær (input_dim, output_dim)
def fremad (selv, x):
vende tilbage selv.lineær (x)

Nu hvor vi er klar med klassen, lad os definere vores model med input og output størrelse på 1:

input_dim = 1
output_dim = 1
model = LinearRegression (input_dim, output_dim)

Vi kan definere MSE som:

mse = nn.MSELoss ((tab))

Vi er klar til at definere den optimering, der kan udføres på modelforudsigelsen for den bedste ydeevne:

# Optimering (find parametre, der minimerer fejl)
learning_rate = 0.02
optimizer = fakkel.optim.SGD (model.parametre (), lr = learning_rate)

Vi kan endelig lave et plot for tabsfunktionen på vores model:

loss_list = []
iteration_number = 1001
for iteration inden for rækkevidde (iteration_number):
# udfør optimering med nul gradient
optimering.zero_grad ()
resultater = model (house_price_tensor)
tab = mse (resultater, hus_størrelse_tensor)
# beregne afledte ved at gå baglæns
tab.baglæns()
# Opdatering af parametre
optimering.trin()
# tab af butik
tab_liste.tilføje (tab.data)
# udskrivningstab
hvis (iteration% 50 == 0):
print ('epoke , tab '.format (iteration, tab.data))
plt.plot (interval (iteration_number), loss_list)
plt.xlabel ("Antal gentagelser")
plt.ylabel ("Tab")
plt

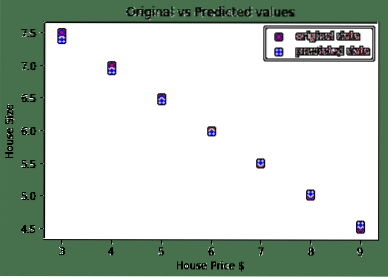
Vi udførte optimeringer flere gange på tabsfunktionen og forsøgte at visualisere, hvor meget tab steg eller faldt. Her er plottet, som er output:

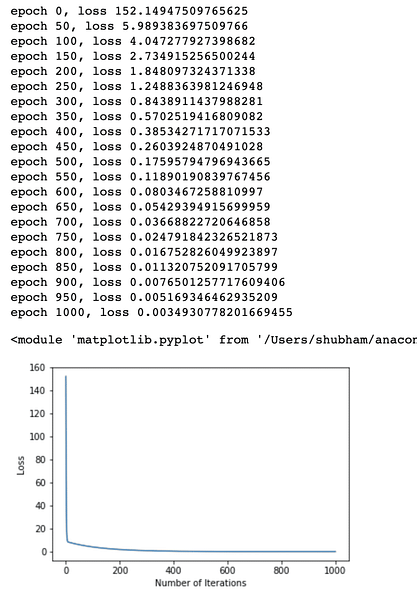
Vi ser, at da antallet af iterationer er højere, har tabet en tendens til nul. Dette betyder, at vi er klar til at forudsige og planlægge det:

# forudsige vores bilpris
forudsagt = model (house_price_tensor).data.bedøvet ()
plt.scatter (house_prices_array, house_size, label = "original data", color = "red")
plt.scatter (house_prices_array, predicted, label = "predicted data", color = "blue")
plt.legende()
plt.xlabel ("Huspris $")
plt.ylabel ("Husstørrelse")
plt.titel ("Original vs forudsagte værdier")
plt.at vise()

Her er plottet, som vil hjælpe os med at forudsige:

Konklusion

I denne lektion så vi på en fremragende beregningspakke, der giver os mulighed for at forudsige hurtigere og effektive forudsigelser og meget mere. PyTorch er populær på grund af den måde, det giver os mulighed for at styre neurale netværk på en grundlæggende måde med Tensors.