Som SciPy er open source, det har et meget aktivt og levende samfund af udviklere, som der findes et enormt antal moduler til en lang række videnskabelige applikationer og beregninger til rådighed med SciPy. Nogle af de komplekse matematiske operationer, der kan udføres med SciPy, er:
- Interpolation
- Integration
- Optimering
- Billedbehandling
- Statistikker
- Specielle funktionsberegninger mv.
SciPy kan sammenlignes med de fleste kommando- og standardbiblioteker som GSL-bibliotek til C ++ og Matlab. Da SciPy er bygget oven på NumPy-pakken, kan disse to pakker også integreres fuldstændigt. Hvis du kan tænke på en matematisk operation, der skal udføres, skal du sørge for at tjekke SciPy-biblioteket, før du implementerer dette modul på egen hånd, fordi SciPy i de fleste tilfælde allerede har alle de operationer, du har implementeret.
Installer SciPy-biblioteket
Lad os installere SciPy-biblioteket, inden vi går til de faktiske eksempler og koncepter. Der er to måder at installere denne pakke på. Den første inkluderer brug af Python pakkehåndtering, pip:
pip install scipyDen anden måde vedrører Anaconda, vi kan installere pakken som:
conda install -c anaconda scipyNår biblioteket er installeret, kan vi importere det som:
importer scipyEndelig, da vi også bruger NumPy (Det anbefales, at vi til alle NumPy-operationer bruger NumPy direkte i stedet for at gå gennem SciPy-pakken):
import bedøvetDet er muligt, at vi i nogle tilfælde også vil plotte vores resultater, som vi vil bruge Matplotlib-biblioteket til. Udfør følgende import for det pågældende bibliotek:
importer matplotlibJeg bruger Anaconda-manager til alle eksemplerne i denne lektion. Jeg lancerer en Jupyter Notebook til det samme:

Nu hvor vi er klar med alle importudtalelser til at skrive en kode, lad os begynde at dykke ned i SciPy-pakken med nogle praktiske eksempler.
Arbejde med polynomiske ligninger
Vi starter med at se på enkle polynomiske ligninger. Der er to måder, hvorpå vi kan integrere polynomiske funktioner i vores program. Vi kan gøre brug af poly1d klasse, der bruger koefficienter eller rødderne til et polynom til initialisering af et polynom. Lad os se på et eksempel:
fra følelsesløs import poly1dfirst_polynomial = poly1d ([3, 4, 7])
udskriv (første_polynom)
Når vi kører dette eksempel, ser vi følgende output:

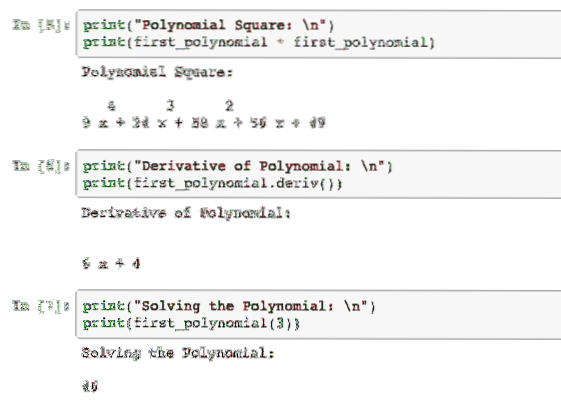
Det er klart, at ligningens polynomrepræsentation er udskrevet som output, så resultatet er ret let at forstå. Vi kan også udføre forskellige operationer på dette polynom, som at kvadratere det, finde dets afledte eller endda løse det til en værdi på x. Lad os prøve at gøre alle disse i det næste eksempel:
print ("Polynomial Square: \ n")udskriv (første_polynom * første_polynom)
print ("Derivat af polynom: \ n")
udskriv (første_polynom.deriv ())
print ("Løsning af polynomet: \ n")
udskriv (første_polynom (3))
Når vi kører dette eksempel, ser vi følgende output:
Lige da jeg tænkte, at dette var alt, hvad vi kunne gøre med SciPy, huskede jeg, at vi også kan integrere et polynom. Lad os køre et sidste eksempel med polynomier:
print ("Integrering af polynomet: \ n")udskriv (første_polynom.integ (1))
Det heltal, vi passerer, fortæller pakken, hvor mange gange polynomet skal integreres:
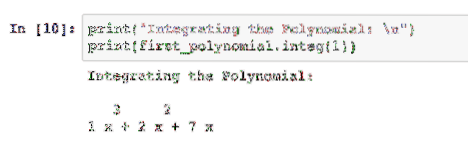
Vi kan simpelthen passere et andet heltal, der fortæller pakken, hvor mange gange der skal integreres dette polynom.
Løsning af lineære ligninger
Det er endda muligt at løse lineære ligninger med SciPy og finde deres rødder, hvis de findes. For at løse lineære ligninger repræsenterer vi sættet med ligninger som NumPy-arrays og deres løsning som separate NumPy-arrays. Lad os visualisere det med et eksempel, hvor vi gør det samme og bruger linalg pakke for at finde ligningens rødder, her er ligningerne, vi skal løse:
1x + 5y = 63x + 7y = 9
Lad os løse ovenstående ligninger:
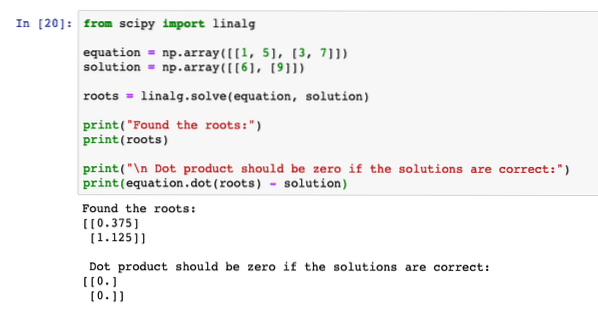
fra scipy import linalgligning = np.matrix ([[1, 5], [3, 7]])
opløsning = np.array ([[6], [9]])
rødder = linalg.løse (ligning, løsning)
print ("Fundet rødderne:")
print (rødder)
print ("\ n Punktprodukt skal være nul, hvis løsningerne er korrekte:")
udskriv (ligning.prik (rødder) - løsning)
Når vi kører ovenstående program, vil vi se, at punktproduktligningen giver nul resultat, hvilket betyder, at de rødder, som programmet fandt, var korrekte:
Fourier-transformationer med SciPy
Fourier Transformations hjælper os med at udtrykke en funktion som separate komponenter, der udgør den funktion, og guider os om den måde, hvorpå vi kan rekombinere disse komponenter for at få den oprindelige funktion tilbage.
Lad os se på et simpelt eksempel på Fourier-transformationer, hvor vi tegner summen af to cosinus ved hjælp af Matplotlib-biblioteket:
fra scipy.fftpack import fft# Antal prøvepunkter
N = 500
# prøveafstand
T = 1.0/800.0
x = np.linspace (0.0, N * T, N)
y = np.cos (50.0 * 2.0 * np.pi * x) + 0.5 * np.cos (80.0 * 2.0 * np.pi * x)
yf = fft (y)
xf = np.linspace (0.0, 1.0 / (2.0 * T), N // 2)
# matplotlib til plotning
importer matplotlib.pyplot som plt
plt.plot (xf, 2.0 / N * np.abs (yf [0: N // 2]))
plt.titel ('Info')
plt.ylabel ('Y-akse')
plt.xlabel ('X-akse')
plt.gitter ()
plt.at vise()
Her startede vi med at konstruere en prøveplads og cosinusligning, som vi derefter transformerede og plottede. Her er output fra ovenstående program:
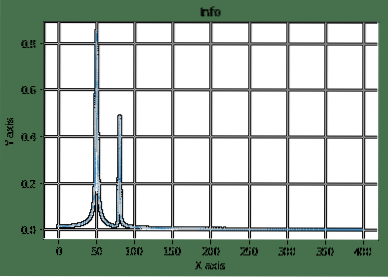
Dette er et af de gode eksempler, hvor vi ser SciPy bruges i en kompleks matematisk ligning til nemt at visualisere tingene.
Vektorer og matrix med SciPy
Nu hvor vi ved en masse ting, som SciPy er i stand til, kan vi være sikre på, at SciPy også kan arbejde med vektorer og matrix. Matricerne er en vigtig del af lineær algebra, da matricer også er noget, vi bruger til at repræsentere Vector-kortlægninger.
Ligesom vi så på at løse lineære ligninger med SciPy, kan vi repræsentere vektorer med np.matrix () funktioner. Lad os starte med at konstruere en matrix:
my_matrix = np.matrix (np.tilfældig.tilfældig ((3, 3)))udskriv (my_matrix)
Her er output fra ovenstående uddrag:

Hver gang vi taler om matricer, taler vi altid om Eigenvalues og Eigenvectors. For at sætte med enkle ord er Eigenvektorer de vektorer, der, når de multipliceres med en matrix, ikke ændrer deres retning i modsætning til de fleste af vektorerne. Dette betyder, at selv når du multiplicerer en Eigenvectors med en matrix, findes der en værdi (eller egenværdi), som er en af multiplikationsfaktoren. Det betyder:
Axe = λx.I ovenstående ligning er A matrixen, λ er Eigenværdien og x er vektoren. Lad os skrive et simpelt kodestykke for at finde Eigenvalues for en given Vector:
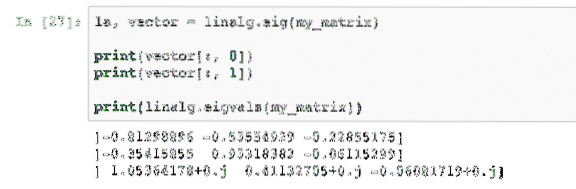
la, vektor = linalg.eig (my_matrix)print (vektor [:, 0])
print (vektor [:, 1])
print (linalg.ejvals (my_matrix))
Når vi kører dette eksempel, ser vi følgende output:
Beregning af matrixdeterminant
Den næste operation, vi udfører med SciPy, er at beregne determinanten for en 2-dimensionel matrix. Vi genbruger den matrix, vi brugte i det sidste kodestykke her:
linalg.det (min_matrix)Når vi kører dette eksempel, ser vi følgende output:

Konklusion
I denne lektion så vi på mange gode eksempler, hvor SciPy kan hjælpe os ved at udføre komplekse matematiske beregninger for os med en brugervenlig API og pakker.
 Phenquestions
Phenquestions