Koden til denne blog sammen med datasættet er tilgængelig på følgende link https: // github.com / shekharpandey89 / k-betyder
K-Means-klyngedannelse er en ikke-overvåget algoritme til maskinindlæring. Hvis vi sammenligner K-Means ikke-overvåget klyngealgoritme med den overvågede algoritme, er det ikke nødvendigt at træne modellen med de mærkede data. K-Means algoritme bruges til at klassificere eller gruppere forskellige objekter baseret på deres attributter eller funktioner i et K antal grupper. Her er K et heltal. K-midlerne beregner afstanden (ved hjælp af afstandsformlen) og finder derefter den mindste afstand mellem datapunkterne og centroid-klyngen for at klassificere dataene.
Lad os forstå K-midlerne ved hjælp af det lille eksempel ved hjælp af de 4 objekter, og hvert objekt har 2 attributter.
| Objektnavn | Attribut_X | Attribut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-midler til løsning af numerisk eksempel:
For at løse ovenstående numeriske problem gennem K-midler skal vi følge følgende trin:
K-Means-algoritmen er meget enkel. Først skal vi vælge et vilkårligt antal K og derefter vælge klyngens centroider eller centrum. For at vælge centroiderne kan vi vælge et vilkårligt antal objekter til initialiseringen (afhænger af værdien af K).
K-Means-algoritmens grundlæggende trin er som følger:
- Fortsætter med at køre, indtil ingen genstande bevæger sig fra deres centroider (stabil).
- Vi vælger først tilfældigt nogle centroider.
- Derefter bestemmer vi afstanden mellem hvert objekt og centroider.
- Gruppering af objekterne baseret på den mindste afstand.
Så hvert objekt har to punkter som X og Y, og de repræsenterer på grafområdet som følger:
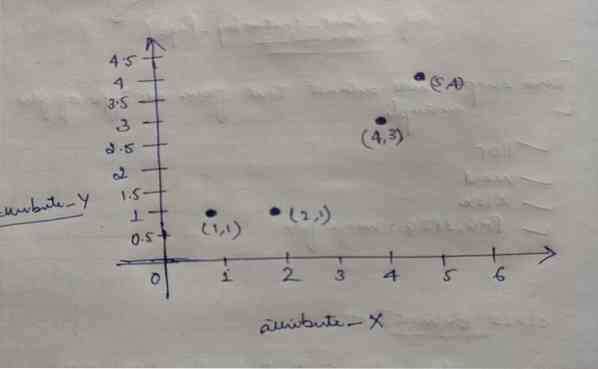
Så vi vælger oprindeligt værdien af K = 2 som tilfældig for at løse vores ovenstående problem.
Trin 1: Oprindeligt vælger vi de to første objekter (1, 1) og (2, 1) som vores centroider. Grafen nedenfor viser det samme. Vi kalder disse centroider C1 (1, 1) og C2 (2,1). Her kan vi sige, at C1 er gruppe_1 og C2 er gruppe_2.
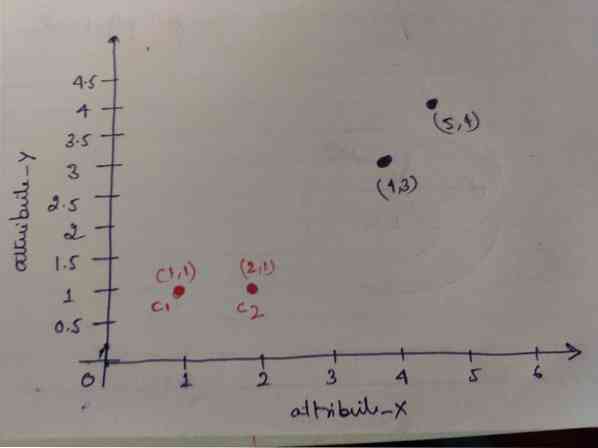
Trin 2: Nu beregner vi hvert objektdatapunkt til centroider ved hjælp af den euklidiske afstandsformel.
For at beregne afstanden bruger vi følgende formel.

Vi beregner afstanden fra objekter til centroider, som vist i nedenstående billede.

Så vi beregnede hver objektdatapunktafstand gennem ovenstående afstandsmetode og fik endelig afstandsmatrixen som angivet nedenfor:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klynge1 | gruppe_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) klynge2 | gruppe_2 |
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Nu har vi beregnet hvert objekts afstandsværdi for hver centroid. For eksempel har objektpunkterne (1,1) en afstandsværdi til c1 er 0 og c2 er 1.
Da vi fra ovenstående afstandsmatrix finder ud af, at objektet (1, 1) har en afstand til klynge1 (c1) er 0 og til klynge2 (c2) er 1. Så objektet en er tæt på selve cluster1.
Tilsvarende, hvis vi kontrollerer objektet (4, 3), er afstanden til klynge1 3.61 og til cluster2 er 2.83. Så objektet (4, 3) skifter til klynge2.
Tilsvarende, hvis du kontrollerer for objektet (2, 1), er afstanden til klynge1 1 og til klynge2 er 0. Så dette objekt skifter til cluster2.
I henhold til deres afstandsværdi grupperer vi punkterne (objektklynger).
G_0 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | gruppe_1 |
| 0 | 1 | 1 | 1 | gruppe_2 |
I henhold til deres afstandsværdi grupperer vi punkterne (objektklyngedannelse).
Og endelig vil grafen se ud som nedenfor efter at have lavet klyngen (G_0).
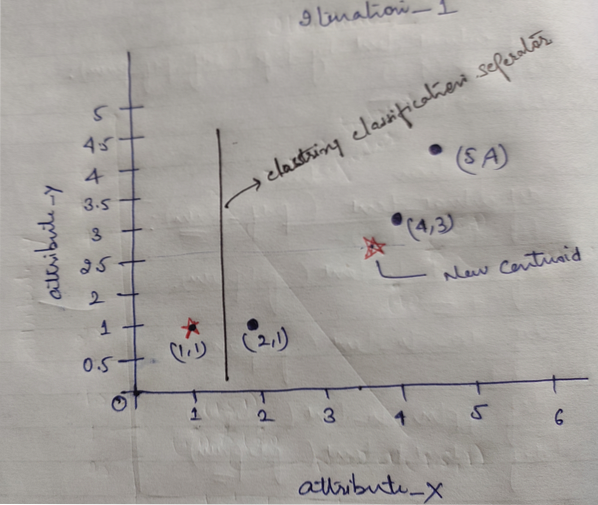
Iteration_1: Nu beregner vi nye centroider, når de oprindelige grupper blev ændret på grund af afstandsformlen som vist i G_0. Så group_1 har kun et objekt, så dets værdi er stadig c1 (1,1), men group_2 har 3 objekter, så dens nye centroid-værdi er 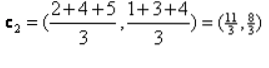
Så nye c1 (1,1) og c2 (3.66, 2.66)
Nu skal vi igen beregne hele afstanden til nye centroider, som vi tidligere har beregnet.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klynge1 | gruppe_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) klynge2 | gruppe_2 |
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (objektklyngedannelse): Nu, på vegne af den nye afstandsmatrix (DM_1) beregning, klynger vi det efter det. Så vi skifter M2-objektet fra group_2 til group_1 som reglen om minimumsafstand til centroids, og resten af objektet vil være den samme. Så ny klyngedannelse vil være som nedenfor.
G_1 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | gruppe_1 |
| 0 | 0 | 1 | 1 | gruppe_2 |
Nu skal vi beregne de nye centroider igen, da begge objekter har to værdier.
Så nye centroider vil være 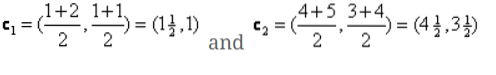
Så når vi har fået de nye centroider, vil klyngen se ud som nedenfor:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
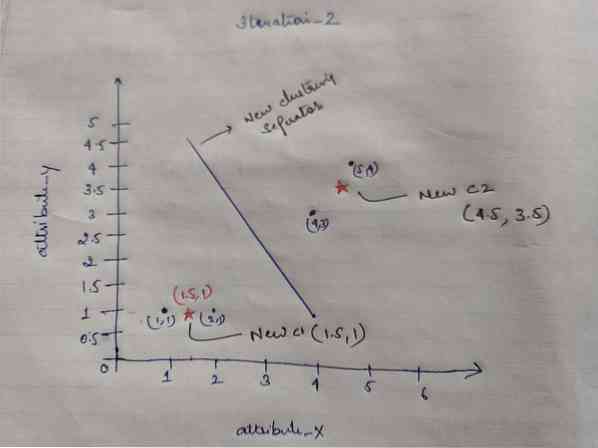
Iteration_2: Vi gentager det trin, hvor vi beregner den nye afstand for hvert objekt til nye beregnede centroider. Så efter beregningen får vi følgende afstandsmatrix til iteration_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) klynge1 | gruppe_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) klynge2 | gruppe_2 |
A B C D
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | x |
| 1 | 1 | 3 | 4 | Y |
Igen udfører vi klyngetildelingerne baseret på den minimale afstand, som vi gjorde før. Så efter at have gjort det, fik vi klyngematricen, som er den samme som G_1.
G_2 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | gruppe_1 |
| 0 | 0 | 1 | 1 | gruppe_2 |
Som her, G_2 == G_1, så der kræves ingen yderligere iteration, og vi kan stoppe her.
K-Means Implementering ved hjælp af Python:
Nu skal vi implementere K-betyder-algoritmen i python. For at implementere K-midlerne skal vi bruge det berømte Iris-datasæt, som er open source. Dette datasæt har tre forskellige klasser. Dette datasæt har grundlæggende fire funktioner: Sepal længde, sepal bredde, kronblad længde og kronblad bredde. Den sidste kolonne fortæller navnet på klassen på den række som setosa.
Datasættet ser ud som nedenfor:
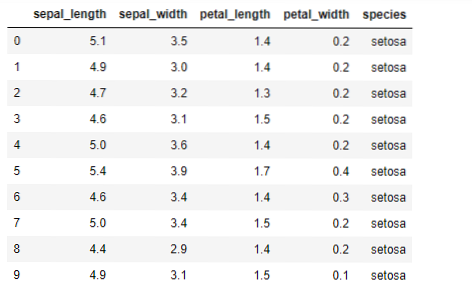
Til implementeringen af python k-betyder er vi nødt til at importere de nødvendige biblioteker. Så vi importerer Pandaer, Numpy, Matplotlib og også KMeans fra sklearn.clutser som angivet nedenfor:

Vi læser Iris.csv-datasæt ved hjælp af read_csv-pandas metode og viser de 10 bedste resultater ved hjælp af hovedmetoden.
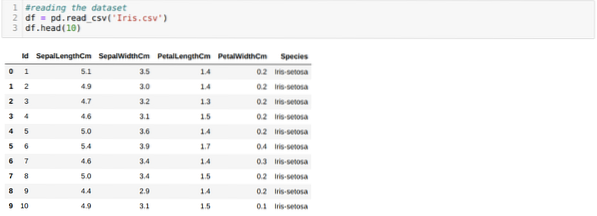
Nu læser vi kun de funktioner i datasættet, som vi krævede for at træne modellen. Så vi læser alle de fire funktioner i datasættene (sepal længde, sepal bredde, kronblad længde, kronblad bredde). Til det overførte vi de fire indeksværdier [0, 1, 2, 3] til iloc-funktionen i pandas dataramme (df) som vist nedenfor:
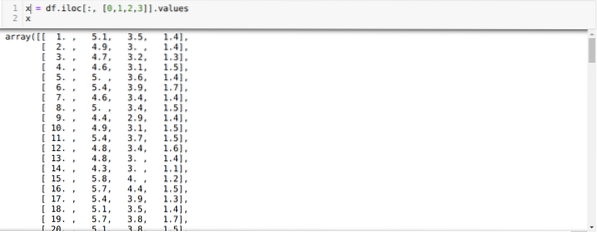
Nu vælger vi antallet af klynger tilfældigt (K = 5). Vi opretter objektet til K-middelklassen og tilpasser derefter vores x-datasæt til det til træning og forudsigelse som vist nedenfor:
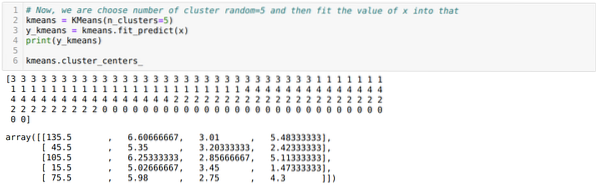
Nu skal vi visualisere vores model med den tilfældige værdi K = 5. Vi kan tydeligt se fem klynger, men det ser ud til, at det ikke er korrekt, som vist nedenfor.
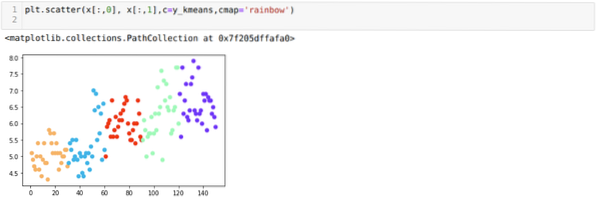
Så vores næste trin er at finde ud af, om antallet af klynger var nøjagtigt eller ej. Og til det bruger vi albuen-metoden. Elbow-metoden bruges til at finde ud af det optimale antal klyngen til et bestemt datasæt. Denne metode vil blive brugt til at finde ud af, om værdien af k = 5 var korrekt eller ej, da vi ikke får klare klynger. Så derefter går vi til følgende graf, som viser, at værdien af K = 5 ikke er korrekt, fordi den optimale værdi falder mellem 3 eller 4.
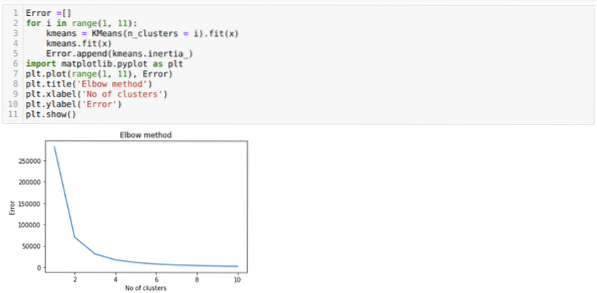
Nu kører vi ovenstående kode igen med antallet af klynger K = 4 som vist nedenfor:
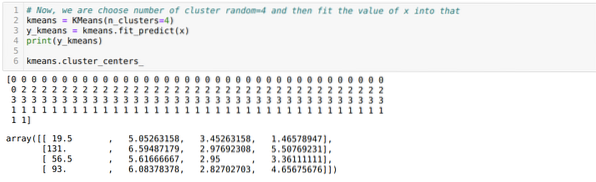
Nu skal vi visualisere ovenstående K = 4 new build-klyngedannelse. Nedenstående skærm viser, at klyngen nu udføres gennem k-middel.
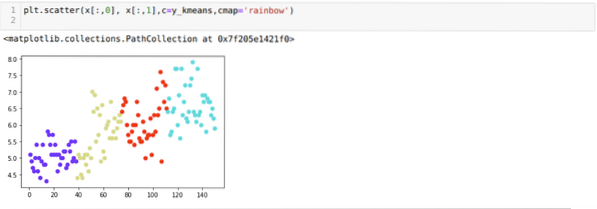
Konklusion
Så vi studerede K-betyder-algoritmen i både numerisk og python-kode. Vi har også set, hvordan vi kan finde ud af antallet af klynger for et bestemt datasæt. Undertiden kan albue-metoden ikke give det korrekte antal klynger, så i så fald er der flere metoder, som vi kan vælge.
 Phenquestions
Phenquestions


